【JavaScript数据结构】二叉树实现

wumanho 收录于技术

2021-12-20 约 1363 字预计阅读 3 分钟

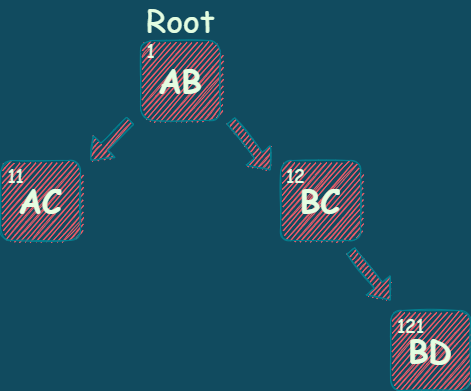
二叉树定义

二叉树由一组相互链接的结点组合而成，最终表示一种具有层次的树形结构。

二叉树中每个结点通过父-子关系互相链接，每一个结点最多拥有两个子结点（即左结点与右结点）。

二叉树中的第一个结点被称为根结点，而没有子结点的结点称为叶子结点。

在二叉树中，每个结点必须具有以下属性：

key：结点的 key
value：结点的值
parent：结点的父节点（如果没有，用null表示）
left：指向结点左子树的指针（如果没有，用null表示）
right：指向结点右子树的指针（如果没有，用null表示）

二叉树的关键操作：

insert：在给定的父结点中插入一个子结点
remove：从二叉树中移除一个结点以及它的子结点
find：检索给定的结点
preOrderTraversal：前序遍历，通过递归遍历每个结点及其子结点来遍历二叉树
postOrderTraversal：后序遍历，从子树最左侧的结点开始，先遍历完叶子结点，再访问父结点，最后访问根结点
inOrderTraversal：中序遍历，最先访问左子树，然后访问根结点，最后访问右子树

实现

结点

创建一个带有构造函数的类表示结点，为每个实例初始化必要属性

1
2
3
4
5
6
7
8
9


class BinaryTreeNode {
  constructor(key, value = key, parent = null) {
    this.key = key
    this.value = value
    this.parent = parent
    this.left = null
    this.right = null
  }
}

定义一个 getter isLeaf，用于检查left和right属性是否为空

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class BinaryTreeNode {
  constructor(key, value = key, parent = null) {
    this.key = key
    this.value = value
    this.parent = parent
    this.left = null
    this.right = null
  }
    
  get isLeaf() {
    return this.left === null && this.right === null
  }
}

定义一个 getter hasChildren，与isLeaf正好相反，所以可以利用isLeaf来判断是否拥有至少一个子结点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class BinaryTreeNode {
  constructor(key, value = key, parent = null) {
    this.key = key
    this.value = value
    this.parent = parent
    this.left = null
    this.right = null
  }

  get isLeaf() {
    return this.left === null && this.right === null
  }

  get hasChildren() {
    return !this.isLeaf
  }
}

树

创建一个带有构造函数的类表示二叉树，为每个实例初始化根节点

1
2
3
4
5


class BinaryTree {
  constructor(key, value = key) {
    this.root = new BinaryTreeNode(key, value)
  }
}

创建生成器方法：

生成器方法主要用于三种遍历的实现，通过yield*语法便可以简单实现递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class BinaryTree {
  constructor(key, value = key) {
    this.root = new BinaryTreeNode(key, value)
  }
    
  *inOrderTraversal(node = this.root) {
    if (node.left) yield* this.inOrderTraversal(node.left)
    yield node
    if (node.right) yield* this.inOrderTraversal(node.right)
  }

  *postOrderTraversal(node = this.root) {
    if (node.left) yield* this.postOrderTraversal(node.left)
    if (node.right) yield* this.postOrderTraversal(node.right)
    yield node
  }

  *preOrderTraversal(node = this.root) {
    yield node
    if (node.left) yield* this.preOrderTraversal(node.left)
    if (node.right) yield* this.preOrderTraversal(node.right)
  }
    
}

创建操作方法：

定义insert()方法，可以复用刚刚完成的构造器方法来遍历查找给定的父结点，并插入一个新的BinaryTreeNode作为左子结点或者右子结点，可以通过参数中传递的option对象来决定
定义remove()方法，可以复用刚刚完成的构造器方法来遍历查找给定的父结点，从二叉树中移除一个BinaryTreeNode
定义find()方法，可以复用刚刚完成的构造器方法来遍历检索给定的结点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65


class BinaryTree {
  constructor(key, value = key) {
    this.root = new BinaryTreeNode(key, value)
  }

  *inOrderTraversal(node = this.root) {
    if (node.left) yield* this.inOrderTraversal(node.left)
    yield node
    if (node.right) yield* this.inOrderTraversal(node.right)
  }

  *postOrderTraversal(node = this.root) {
    if (node.left) yield* this.postOrderTraversal(node.left)
    if (node.right) yield* this.postOrderTraversal(node.right)
    yield node
  }

  *preOrderTraversal(node = this.root) {
    yield node
    if (node.left) yield* this.preOrderTraversal(node.left)
    if (node.right) yield* this.preOrderTraversal(node.right)
  }

  insert(
    parentNodeKey,key,value = key,
    { left, right } = { left: true, right: true }) {
    for (let node of this.preOrderTraversal()) {
      if (node.key === parentNodeKey) {
        const canInsertLeft = left && node.left === null
        const canInsertRight = right && node.right === null
        if (!canInsertLeft && !canInsertRight) return false
        if (canInsertLeft) {
          node.left = new BinaryTreeNode(key, value, node)
          return true
        }
        if (canInsertRight) {
          node.right = new BinaryTreeNode(key, value, node)
          return true
        }
      }
    }
    return false
  }

  remove(key) {
    for (let node of this.preOrderTraversal()) {
      if (node.left.key === key) {
        node.left = null
        return true
      }
      if (node.right.key === key) {
        node.right = null
        return true
      }
    }
    return false
  }

  find(key) {
    for (let node of this.preOrderTraversal()) {
      if (node.key === key) return node
    }
    return undefined
  }
}

（完）

目录